Tutorial Wavelet Transform Pdf

Basics of Wavelets Referenc Daubechies (Ten Lectes: I. Waveletsures on; Orthonormal Bases of Compactly Supported Wavelets). The wavelet transform.
THE ULTIMATE SOLUTION: THE WAVELET TRANSFORM The Wavelet transform is a transform of this type. It provides the time-frequency representation. (There are other transforms which give this information too, such as short time Fourier transform, Wigner distributions, etc.) Often times a particular spectral component occurring at any instant can be of particular interest. In these cases it may be very beneficial to know the time intervals these particular spectral components occur. For example, in EEGs, the latency of an event-related potential is of particular interest (Event-related potential is the response of the brain to a specific stimulus like flash-light, the latency of this response is the amount of time elapsed between the onset of the stimulus and the response). Wavelet transform is capable of providing the time and frequency information simultaneously, hence giving a time-frequency representation of the signal. How wavelet transform works is completely a different fun story, and should be explained after short time Fourier Transform (STFT ).
The WT was developed as an alternative to the STFT. The STFT will be explained in great detail in the second part of this tutorial. It suffices at this time to say that the WT was developed to overcome some resolution related problems of the STFT, as explained in Part II. To make a real long story short, we pass the time-domain signal from various highpass and low pass filters, which filters out either high frequency or low frequency portions of the signal. This procedure is repeated, every time some portion of the signal corresponding to some frequencies being removed from the signal. Here is how this works: Suppose we have a signal which has frequencies up to 1000 Hz.
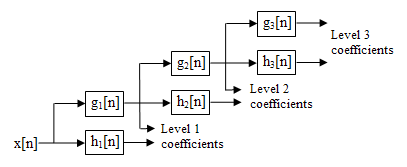
In the first stage we split up the signal in to two parts by passing the signal from a highpass and a lowpass filter (filters should satisfy some certain conditions, so-called admissibility condition) which results in two different versions of the same signal: portion of the signal corresponding to 0-500 Hz (low pass portion), and 500-1000 Hz (high pass portion). Then, we take either portion (usually low pass portion) or both, and do the same thing again. This operation is called decomposition. Assuming that we have taken the lowpass portion, we now have 3 sets of data, each corresponding to the same signal at frequencies 0-250 Hz, 250-500 Hz, 500-1000 Hz.
Then we take the lowpass portion again and pass it through low and high pass filters; we now have 4 sets of signals corresponding to 0-125 Hz, 125-250 Hz,250-500 Hz, and 500-1000 Hz. We continue like this until we have decomposed the signal to a pre-defined certain level. Then we have a bunch of signals, which actually represent the same signal, but all corresponding to different frequency bands. We know which signal corresponds to which frequency band, and if we put all of them together and plot them on a 3-D graph, we will have time in one axis, frequency in the second and amplitude in the third axis. This will show us which frequencies exist at which time ( there is an issue, called 'uncertainty principle', which states that, we cannot exactly know what frequency exists at what time instance, but we can only know what frequency bands exist at what time intervals, more about this in the subsequent parts of this tutorial). However, I still would like to explain it briefly: The uncertainty principle, originally found and formulated by Heisenberg, states that, the momentum and the position of a moving particle cannot be known simultaneously. This applies to our subject as follows: The frequency and time information of a signal at some certain point in the time-frequency plane cannot be known.
In other words: We cannot know what spectral component exists at any given time instant. The best we can do is to investigate what spectral components exist at any given interval of time.
This is a problem of resolution, and it is the main reason why researchers have switched to WT from STFT. STFT gives a fixed resolution at all times, whereas WT gives a variable resolution as follows: Higher frequencies are better resolved in time, and lower frequencies are better resolved in frequency. This means that, a certain high frequency component can be located better in time (with less relative error) than a low frequency component. On the contrary, a low frequency component can be located better in frequency compared to high frequency component. Take a look at the following grid: f ^. continuous.
Wavelet Decomposition Tutorial
wavelet transform. time Interpret the above grid as follows: The top row shows that at higher frequencies we have more samples corresponding to smaller intervals of time. In other words, higher frequencies can be resolved better in time. The bottom row however, corresponds to low frequencies, and there are less number of points to characterize the signal, therefore, low frequencies are not resolved well in time.
^frequency. discrete time wavelet transform. time In discrete time case, the time resolution of the signal works the same as above, but now, the frequency information has different resolutions at every stage too. Note that, lower frequencies are better resolved in frequency, where as higher frequencies are not. Note how the spacing between subsequent frequency components increase as frequency increases.
Below, are some examples of continuous wavelet transform: Let's take a sinusoidal signal, which has two different frequency components at two different times: Note the low frequency portion first, and then the high frequency. Figure 1.10 The continuous wavelet transform of the above signal: Figure 1.11 Note however, the frequency axis in these plots are labeled as scale. The concept of the scale will be made more clear in the subsequent sections, but it should be noted at this time that the scale is inverse of frequency. That is, high scales correspond to low frequencies, and low scales correspond to high frequencies.
Coiflet1 Wavelet Transform Pdf
Consequently, the little peak in the plot corresponds to the high frequency components in the signal, and the large peak corresponds to low frequency components ( which appear before the high frequency components in time) in the signal. You might be puzzled from the frequency resolution shown in the plot, since it shows good frequency resolution at high frequencies. Note however that, it is the good scale resolution that looks good at high frequencies (low scales), and good scale resolution means poor frequency resolution and vice versa.
More about this in Part II and III. TO BE CONTINUED. This concludes the first part of this tutorial, where I have tried to give a brief overview of signal processing, the Fourier transform and the wavelet transform. First written: November 1994 Revised: July 23, 1995 Second Edition: June 5, 1996 The Wavelet Tutorial is hosted by Rowan University, College of Engineering Web Servers All Rights Reserved. This tutorial is intended for educational purposes only. Unauthorized copying, duplicating and publishing is strictly prohibited. Robi Polikar 136 Rowan Hall Dept.
Of Electrical and Computer Engineering Rowan University Glassboro, NJ 08028 Phone: (856) 256 5372 E-Mail:.